Algorithms (Catalog)

Data structures

Catalog reference markup

• Dictionaries

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#ds-dictionaries)

• Priority queues

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#ds-priority-queues)

• Suffix trees and arrays

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#ds-suffix-trees-and-arrays)

• Graph data structures

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#ds-graph-data-structures)

• Set data structures

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#ds-set-data-structures)

• Kd-trees

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#ds-kd-trees)

• Solving linear equations

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#np-linear-equations)

• Bandwidth reduction

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#np-bandwidth-reduction)

• Matrix multiplication

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#np-matrix-multiplication)

• Determinants and permanents

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#np-determinants-and-permanents)

• Constrained/unconstrained optimization

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#np-optimization)

• Linear programming

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#np-linear-programming)

• Random number generation

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#np-random-number-generation)

• Factoring and primality testing

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#np-factoring-primality)

• Arbitrary-precision arithmetic

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#np-arithmetic)

• Knapsack problem

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#np-knapsack)

• Discrete Fourier transform

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#np-fourier)

• Sorting

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#cp-sorting)

• Searching

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#cp-searching)

• Median and selection

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#cp-median-selection)

• Generating permutations

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#cp-gen-permutations)

• Generating subsets

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#cp-gen-subsets)

• Generating partitions

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#cp-gen-partitions)

• Generating graphs

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#cp-gen-graphs)

• Calendrical calculations

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#cp-calendar)

• Job scheduling

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#cp-job-scheduling)

• Satisfiability

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#cp-satisfiability)

• Connected components

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#gp-pt-connected-components)

• Topological sorting

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#gp-pt-topological-sorting)

• Minimum spanning tree

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#gp-pt-mst)

• Shortest path

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#gp-pt-shortest-path)

• Transitive closure and reduction

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#gp-pt-transitive)

• Matching

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#gp-pt-matching)

• Eulerian cycle/Chinese postman

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#gp-pt-eulerian-cycle)

• Edge and vertex connectivity

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#gp-pt-edge-vertex-connectivity)

• Network flow

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#gp-pt-network-flow)

• Drawing graphs nicely

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#gp-pt-drawing-graphs)

• Drawing trees

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#gp-pt-drawing-trees)

• Planarity detection and embedding

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#gp-pt-planarity)

• Clique

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#gp-np-clique)

• Independent set

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#gp-np-independent-set)

• Vertex cover

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#gp-np-vertex-cover)

• Traveling salesman problem

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#gp-np-tsp)

• Hamiltonian cycle

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#gp-np-hamiltonian)

• Graph partition

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#gp-np-graph-partition)

• Vertex coloring

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#gp-np-vertex-coloring)

• Edge coloring

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#gp-np-edge-coloring)

• Graph isomorphism

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#gp-np-graph-isomorphism)

• Steiner tree

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#gp-np-steiner-tree)

• Feedback edge/vertex set

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#gp-np-feedback)

• Robust geometric primitives

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#cg-primitives)

• Convex hull

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#cg-convex-hull)

• Triangulation

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#cg-triangulation)

• Voronoi diagrams

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#cg-voronoi)

• Nearest-neighbor search

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#cg-nearest-neighbor)

• Range search

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#cg-range-search)

• Point location

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#cg-point-location)

• Intersection detection

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#cg-intersection-detection)

• Bin packing

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#cg-bin-packing)

• Medial-axis transform

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#cg-medial-axis-transform)

• Polygon partitioning

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#cg-polygon-partitioning)

• Simplifying polygons

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#cg-simplifying-polygons)

• Shape similarity

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#cg-shape-similarity)

• Motion planning

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#cg-motion-planning)

• Maintaining line arrangements

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#cg-line-arrangements)

• Minkowski sum

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#cg-minkowski)

• Set cover

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#ss-set-cover)

• Set packing

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#ss-set-packing)

• String matching

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#ss-string-matching)

• Approximate string matching

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#ss-string-matching-approximate)

• Text compression

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#ss-text-compression)

• Cryptography

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#ss-cryptography)

• Fininte state machine minimization

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#ss-finite-state)

• Longest common substring/subsequence

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#ss-longest-common)

• Shortest common superstring

  [the catalog](/docs/books/algorithm-design-manual/algorithms-catalog#ss-shortest-common)

Dictionaries

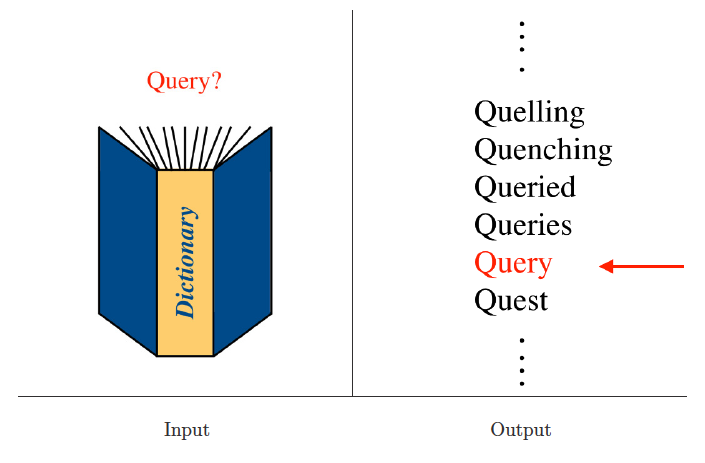
Input description: A set of $n$ records, each identified by one or more keys.

Problem description: Build and maintain a data structure to efficiently locate, insert, and delete the record associated with any query key $q$.

Priority queues

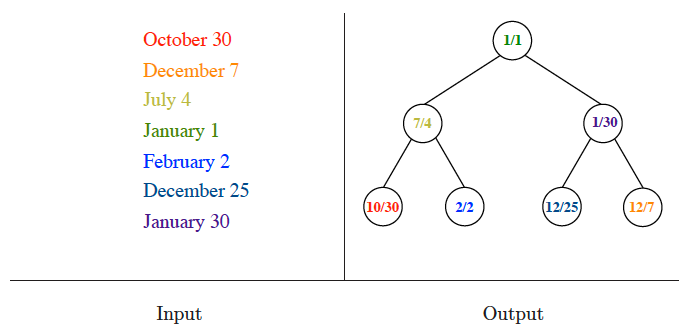
Input description: A set of records with totally ordered keys.

Problem description: Build and maintain a data structure for providing quick access to the smallest or largest key in the set.

Suffix trees and arrays

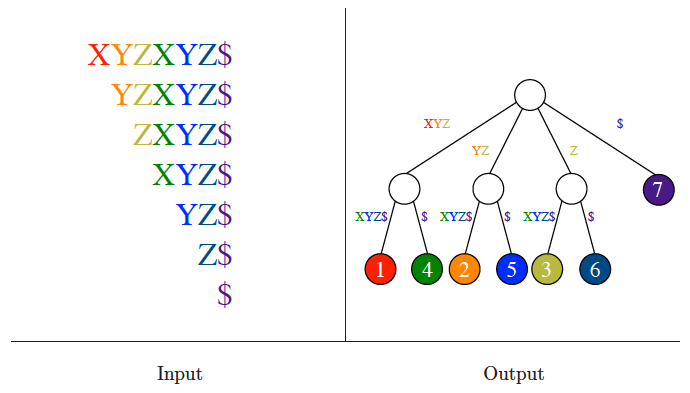
Input description: A reference string $S$.

Problem description: Build a data structure for quickly finding all places where an arbitrary query string $q$ occurs in $S$.

Graph data structures

Input description: A graph $G$.

Problem description: Represent the graph $G$ using a flexible, efficient data structure.

Set data structures

Input description: A universe of items $U=\{u_1,\ldots,u_n\}$ on which is defined a collection of subsets $S=\{S_1,\ldots,S_m\}$.

Problem description: Represent each subset so as to efficiently

1. test whether $u_i\in S_j$,
2. compute the union or intersection of $S_i$ and $S_j$, and
3. insert or delete members of $S$.

Kd-trees

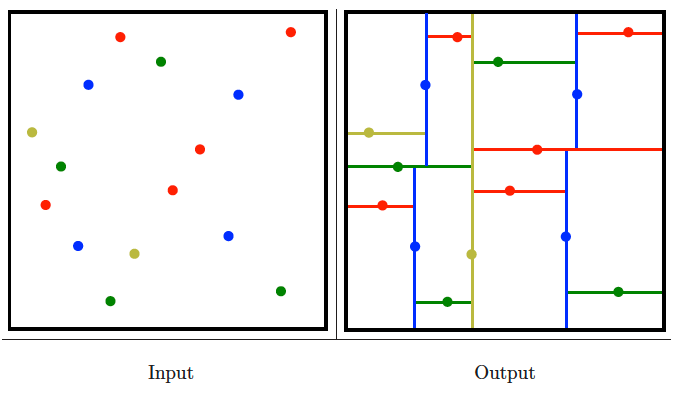
Input description: A set $S$ of $n$ points (or more complicated geometric objects) in $k$ dimensions.

Problem description: Construct a tree that partitions space by half-planes such that each object is contained in its own box-shaped region.

Numerical problems

Solving linear equations

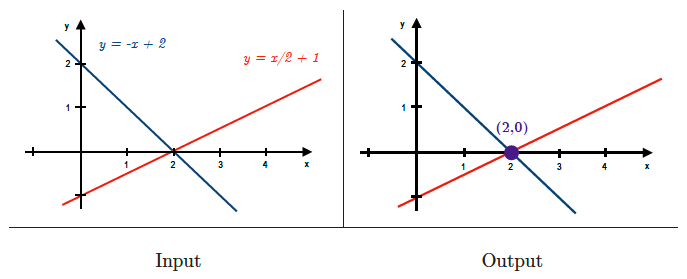
Input description: An $m\times n$ matrix $A$ and an $m\times 1$ vector $b$, together representing $m$ linear equations on $n$ variables.

Problem description: What is the vector $x$ such that $A\cdot x=b$?

Bandwidth reduction

Input description: A graph $G=(V,E)$, representing an $n\times n$ matrix $M$ of zero and non-zero elements.

Problem description: Which permutation $p$ of the vertices minimizes the length of the longest edge--i.e., minimizes $\max_{(i,j)\in E}|p(i)-p(j)|$?

Matrix multiplication

Input description: An $x\times y$ matrix $A$ and a $y\times z$ matrix $B$.

Problem description: Compute the $x\times z$ matrix $A\times B$.

Determinants and permanents

Input description: An $n\times n$ matrix $M$.

Problem description: What is the determinant $|M|$ or permanent $\operatorname{perm}(M)$ of the matrix $M$?

Constrained/unconstrained optimization

Input description: A function $f(x_1,\ldots,x_n)$.

Problem description: Which point $p=(p_1,\ldots,p_n)$ maximizes (or minimizes) the function $f$?

Linear programming

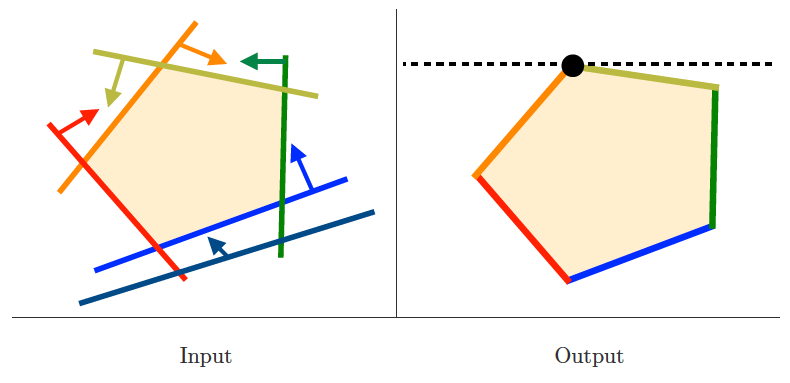
Input description: A set $S$ of $n$ linear inequalities on $m$ variables

$$S_i=\sum_{j=1}^m c_{ij}\cdot x_j\geq b_i,\quad 1\leq i\leq n$$

and a linear optimization function $f(X)=\sum_{j=1}^m c_j\cdot x_j$.

Problem description: Which variable assignment $X'$ maximizes the objective function $f$ while satisfying all inequalities $S$?

Random number generation

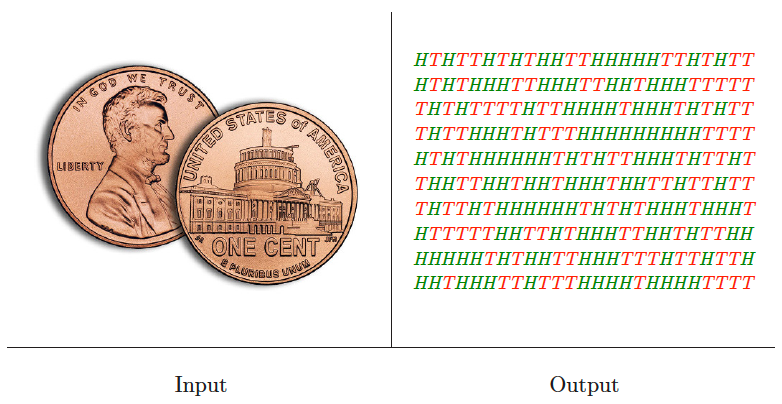
Input description: Nothing, or perhaps a seed.

Problem description: Generate a sequence of random integers.

Factoring and primality testing

Input description: An integer $n$.

Problem description: Is $n$ a prime number? If not, what are its factors?

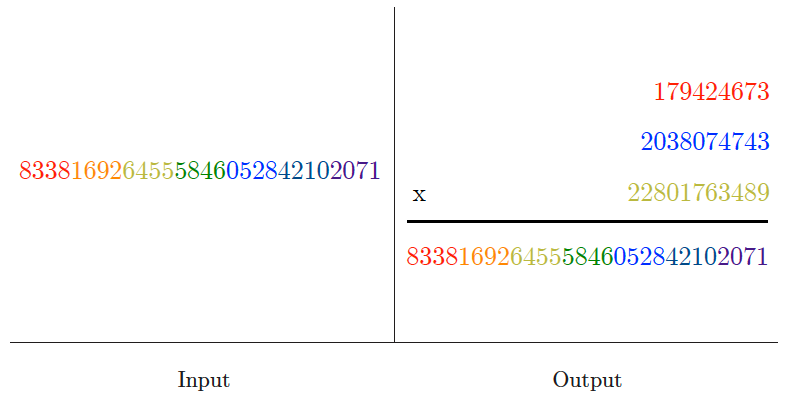
Arbitrary-precision arithmetic

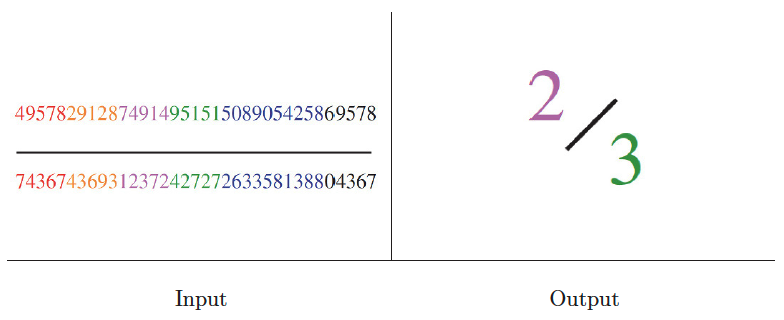
Input description: Two very large integers, $x$ and $y$.

Problem description: What is $x+y$, $x-y$, $x\times y$, and $x/y$?

Knapsack problem

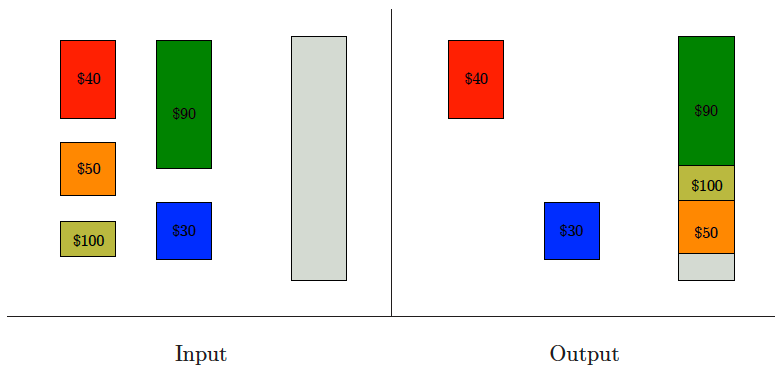
Input description: A set of items $S=\{1,\ldots,n\}$, where item $i$ has size $s_i$ and value $v_i$. A knapsack capacity $C$.

Problem description: Find the subset $S'$ of $S$ that maximizes the value of $\sum_{i\in S'}v_i$ given $\sum_{i\in S'}s_i\leq C$; that is, all the items fit in a knapsack of size $C$.

Discrete Fourier transform

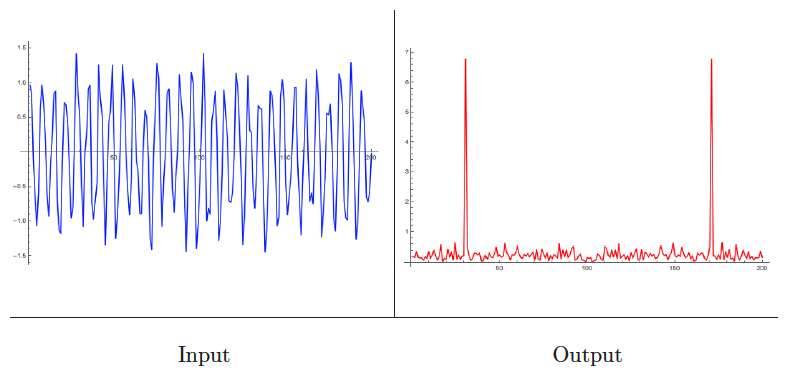
Input description: A sequence of $n$ real or complex values $h_i$, $0\leq i\leq n-1$, sampled at uniform intervals from a function $h$.

Problem description: The discrete Fourier transform $H_m=\sum_{k=0}^{n-1}h_ke^{-2\pi ikm/n}$ for $0\leq m\leq n-1$.

Combinatorial problems

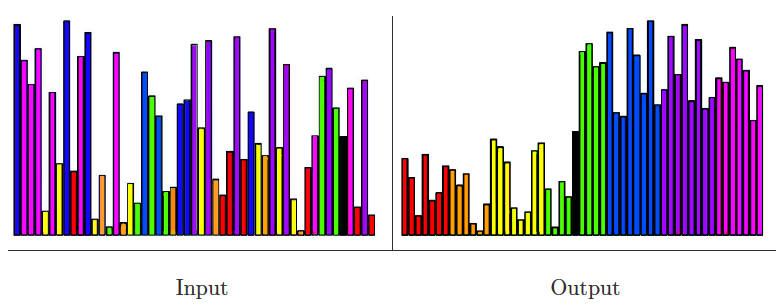
Sorting

Input description: A set of $n$ items.

Problem description: Arrange the items in increasing order.

Searching

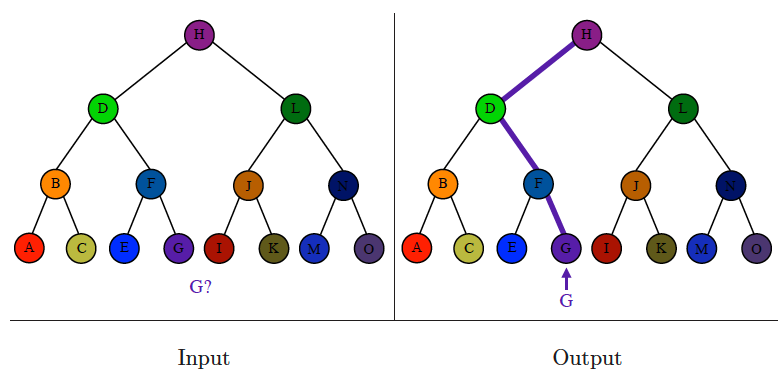
Input description: A set of $n$ keys $S$, and a query key $q$.

Problem description: Where is $q$ in $S$?

Median and selection

Input description: A set of $n$ numbers or keys, and an integer $k$.

Problem description: Find the key greater than or equal to exactly $k$ of the $n$ keys.

Generating permutations

Input description: An integer $n$.

Problem description: Generate

1. all, or
2. a random, or
3. the next permutation of length $n$.

Generating subsets

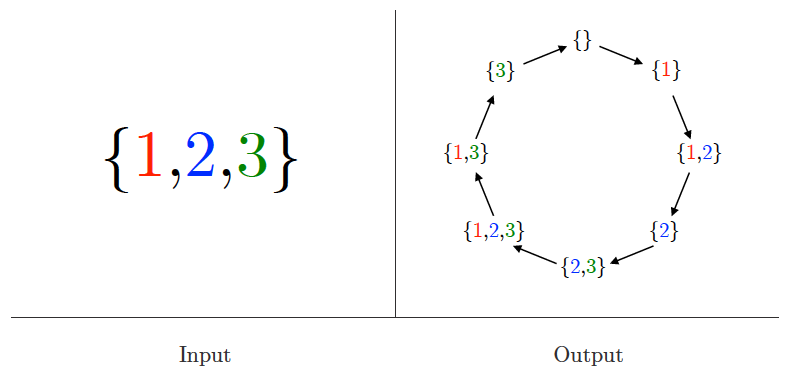
Input description: An integer $n$.

Problem description: Generate

1. all, or
2. a random, or
3. the next subset of the integers $\{1,\ldots,n\}$.

Generating partitions

Input description: An integer $n$.

Problem description: Generate

1. all, or
2. a random, or
3. the next integer or set partitions of length $n$.

Generating graphs

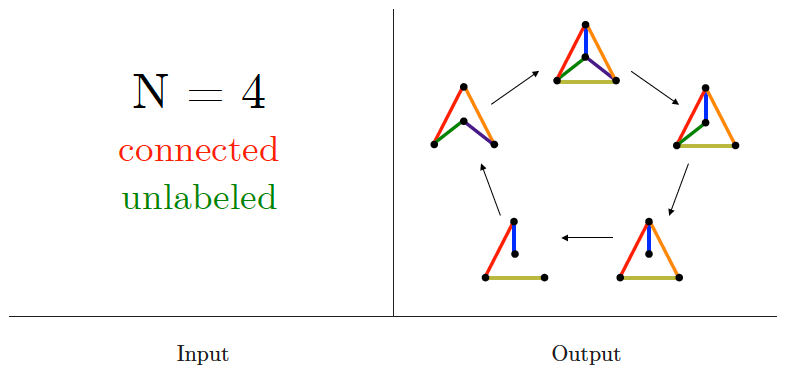
Input description: Parameters describing the desired graph, including the number of vertices $n$, and the number of edges $m$ or edge probability $p$.

Problem description: Generate

1. all, or
2. a random, or
3. the next graph satisfying the parameters.

Calendrical calculations

Input description: A particular calendar date $d$: month, day, and year.

Problem description: Which day of the week did $d$ fall on according to the given calendar system?

Job scheduling

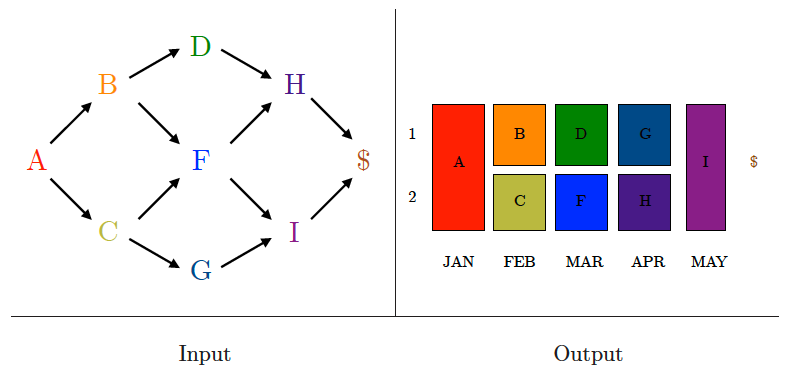
Input description: A directed acyclic graph $G=(V,E)$, with vertices representing jobs, and edge $(u,v)$ implies task $u$ must be done before task $v$.

Problem description: Which schedule of tasks completes the job using the minimum amount of time or processors?

Satisfiability

Input description: A set of clauses in conjunctive normal form.

Problem description: Is there a truth assignment to the Boolean variables such that every clause is simultaneously satisfied?

Graph Problems - Polynomial Time

Connected components

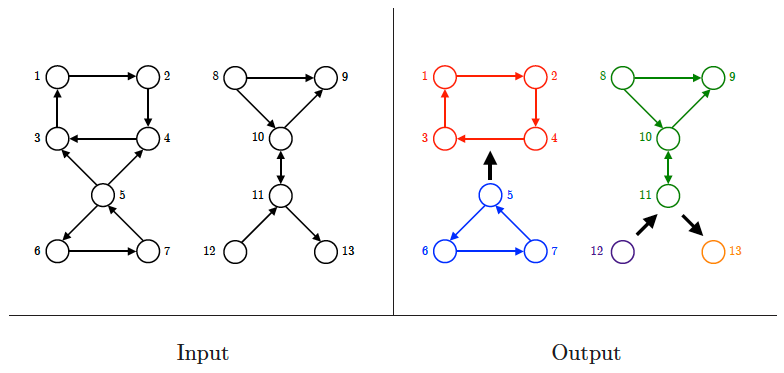
Input description: A directed or undirected graph $G$.

Problem description: Identify the different pieces or components of $G$, where vertices $x$ and $y$ are in different components when no path exists from $x$ to $y$ in $G$.

Topological sorting

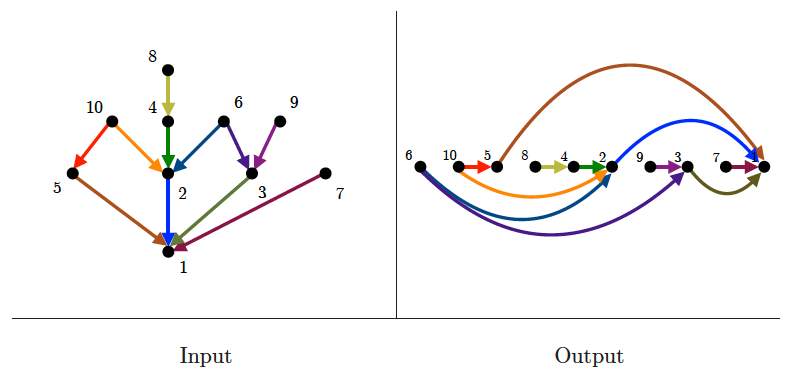
Input description: A directed acyclic graph $G=(V,E)$, also known as a partial order or poset.

Problem description: Find a linear ordering of the vertices of $V$ such that for each edge $(i,j)\in E$, vertex $i$ is to the left of vertex $j$.

Minimum spanning tree

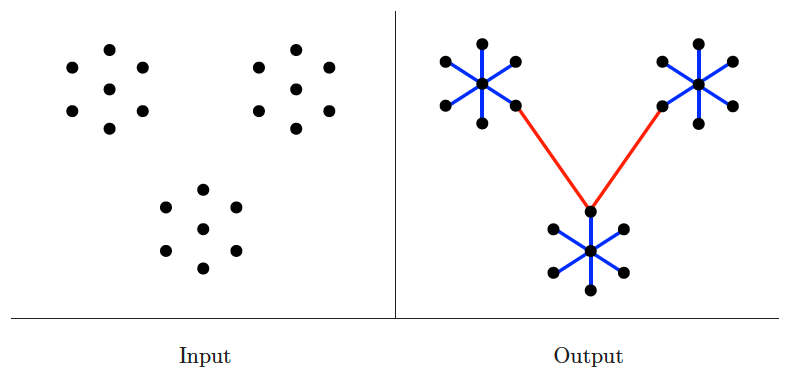
Input description: A graph $G=(V,E)$ with weighted edges.

Problem description: Find a subset of edges $E'\subset E$ that define a tree of minimum weight on $V$.

Shortest path

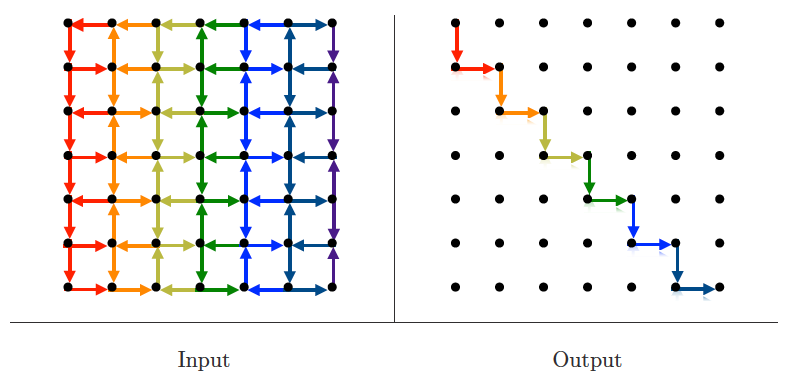
Input description: An edge-weighted graph $G$, with vertices $s$ and $t$.

Problem description: Find the shortest path from $s$ to $t$ in $G$.

Transitive closure and reduction

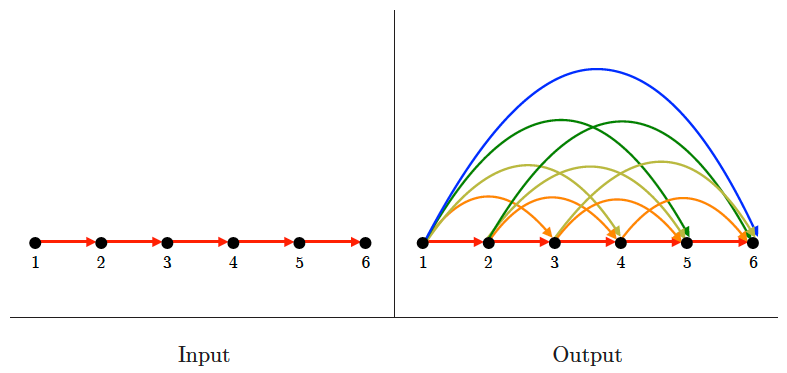
Input description: A directed graph $G=(V,E)$.

Problem description: For transitive closure, construct a graph $G'$  with edge $(i, j)\in E'$ iff there is a directed path from $i$ to $j$ in $G$. For transitive reduction, construct a graph $G'$ with the smallest number of edges such that a directed path from $i$ to $j$ exists in $G'$ iff there is a directed path from $i$ to $j$ in $G$.

Matching

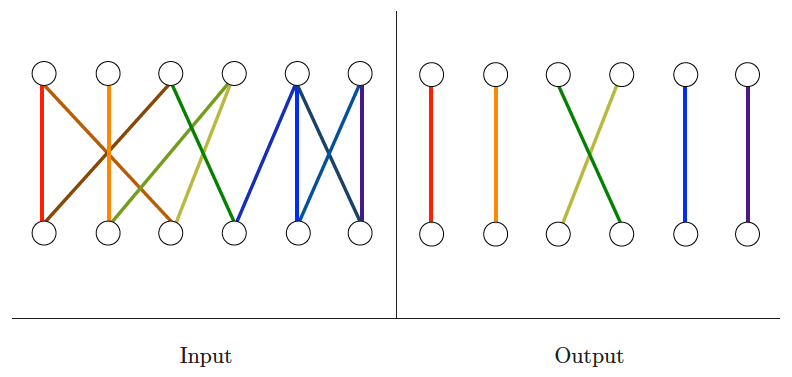
Input description: A (weighted) graph $G = (V,E)$.

Problem description: Find the largest set of edges $E'$ from $E$ such that every vertex in $V$ is incident to at most one edge of $E'$.

Eulerian cycle/Chinese postman

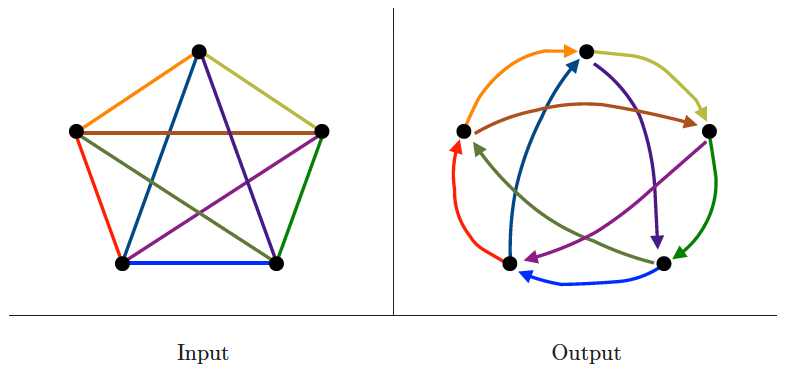
Input description: A graph $G=(V,E)$.

Problem description: Find the shortest tour visiting every edge of $G$.

Edge and vertex connectivity

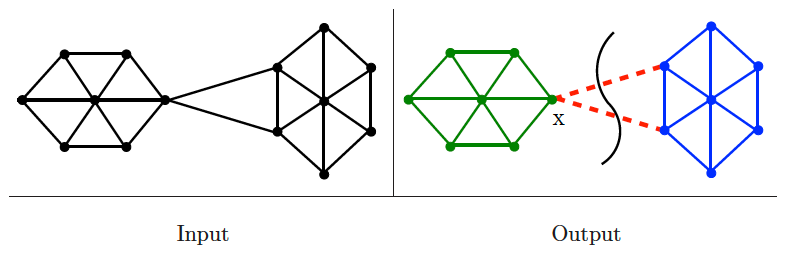
Input description: A graph $G$. Optionally, a pair of vertices $s$ and $t$.

Problem description: What is the smallest subset of vertices (or edges) whose deletion will disconnect $G$, or that will separate $s$ from $t$?

Network flow

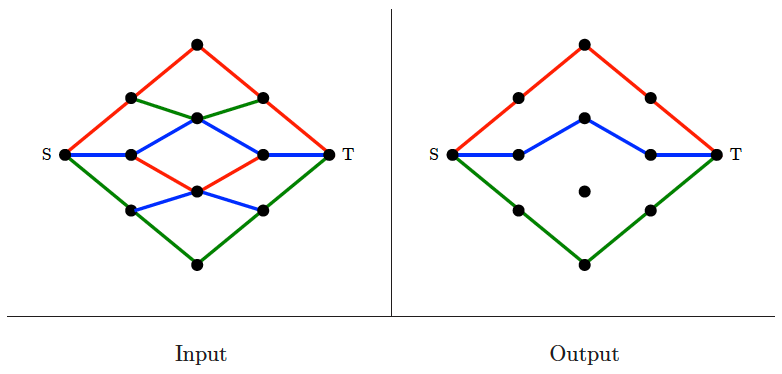
Input description: A directed graph $G$, where each edge $e=(i,j)$ has a capacity $c_e$. A source node $s$ and sink node $t$.

Problem description: What is the maximum flow you can route from $s$ to $t$ while respecting the capacity constraint of each edge?

Drawing graphs nicely

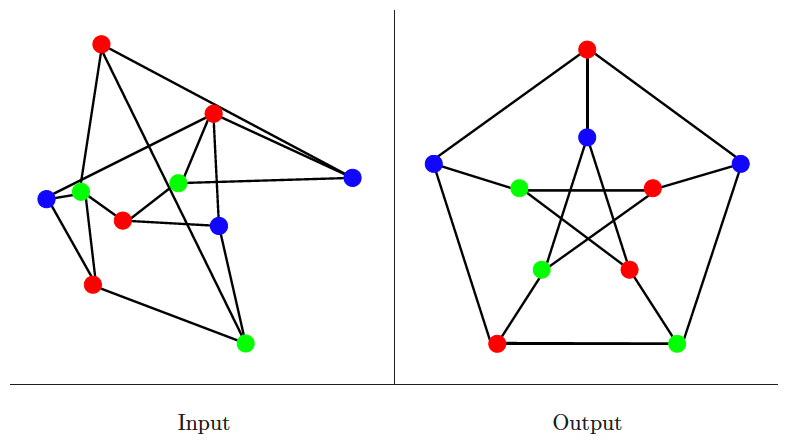
Input description: A graph $G$.

Problem description: Draw a graph $G$ to accurately reflect its structure.

Drawing trees

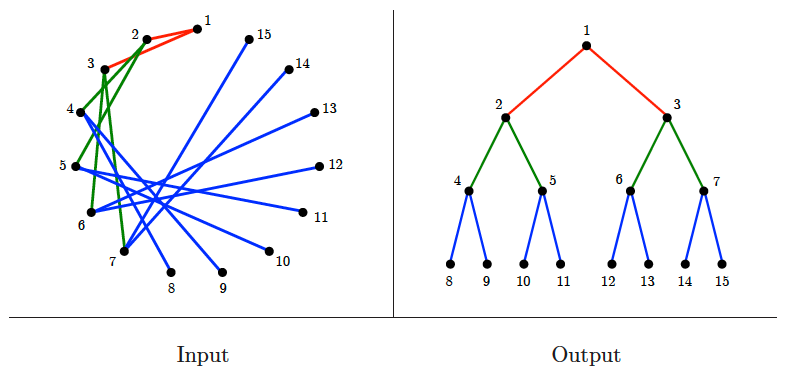
Input description: A tree $T$, which is a graph without any cycles.

Problem description: Create a nice drawing of the tree $T$.

Planarity detection and embedding

Input description: A graph $G$.

Problem description: Can $G$ be drawn in the plane such that no two edges cross? If so, produce such a drawing.

Graph Problems - NP-Hard

Clique

Input description: A graph $G=(V,E)$.

Problem description: What is the largest subset $S$ of vertices such that all pairs are connected, that is, for all $x,y\in S$, $(x,y)\in E$?

Independent set

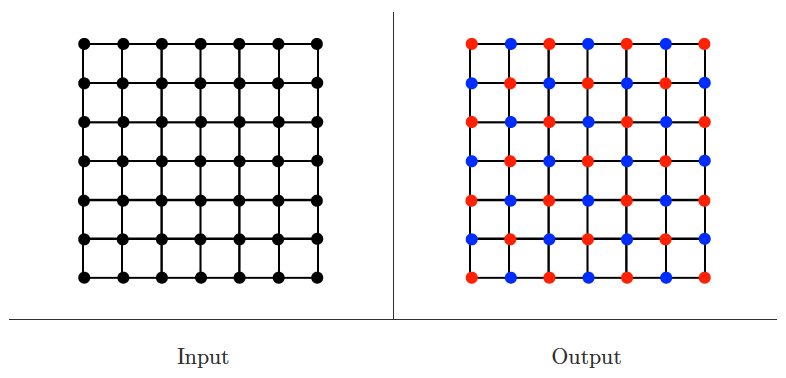
Input description: A graph $G=(V,E)$.

Problem description: What is the largest subset $S$ of vertices $V$ such that there is no edge $(x,y)\in E$ where $x\in S$ and $y\in S$?

Vertex cover

Input description: A graph $G=(V,E)$.

Problem description: What is the smallest subset $C\subseteq V$ such that every edge $(x,y)\in E$ contains at least one vertex of $C$?

Traveling salesman problem

Input description: A weighted graph $G$.

Problem description: Find the cycle of minimum cost, visiting each vertex of $G$ exactly once.

Hamiltonian cycle

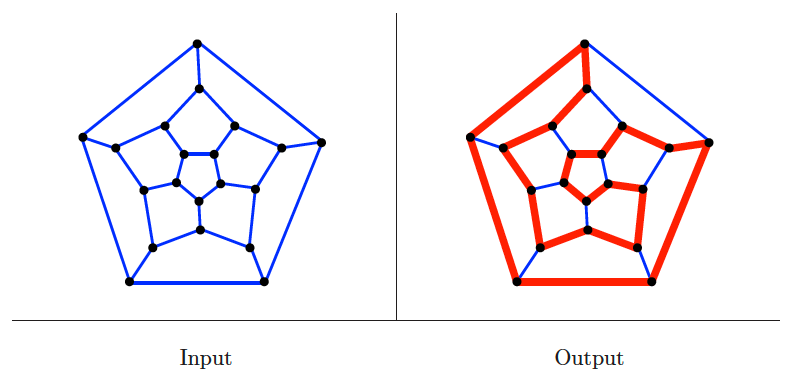
Input description: A graph $G=(V,E)$.

Problem description: Find a tour of the vertices using only edges from $G$, such that each vertex is visited exactly once.

Graph partition

Input description: A (weighted) graph $G=(V,E)$ and integers $k$ and $m$.

Problem description: Partition the vertices into $m$ roughly equal-sized subsets such that the total cost of edges spanning the subsets is at most $k$.

Vertex coloring

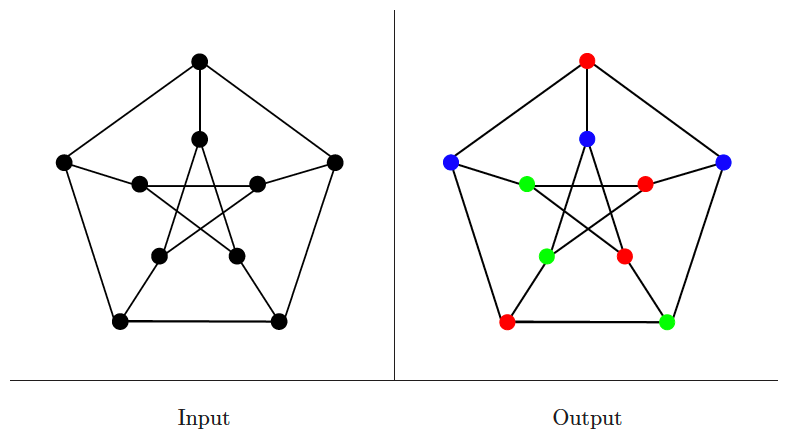
Input description: A graph $G=(V,E)$.

Problem description: Color the vertices of $V$ using the minimum number of colors such that for all $(i,j)\in E$, vertices $i$ and $j$ have different colors.

Edge coloring

Input description: A graph $G=(V,E)$.

Problem description: What is the smallest set of colors needed to color the edges of $G$ such that no two edges of the same color share a common vertex?

Graph isomorphism

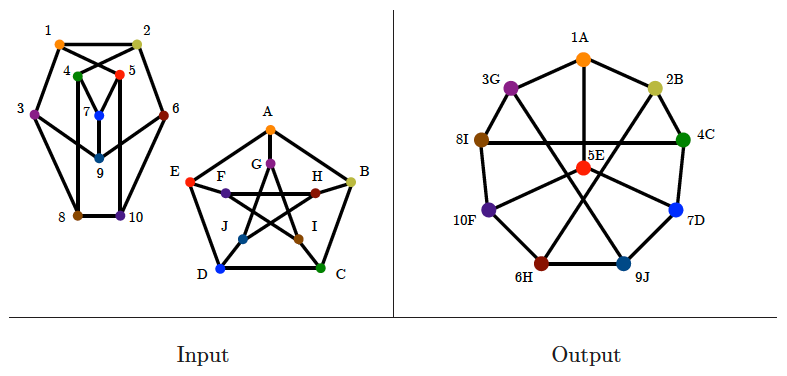
Input description: Two graphs, $G$ and $H$.

Problem description: Find a mapping $f$ from the vertices of $G$ to the vertices of $H$ such that $G$ and $H$ are identical, that is, $(x,y)$ is an edge of $G$ iff $(f(x),f(y))$ is an edge of $H$.

Steiner tree

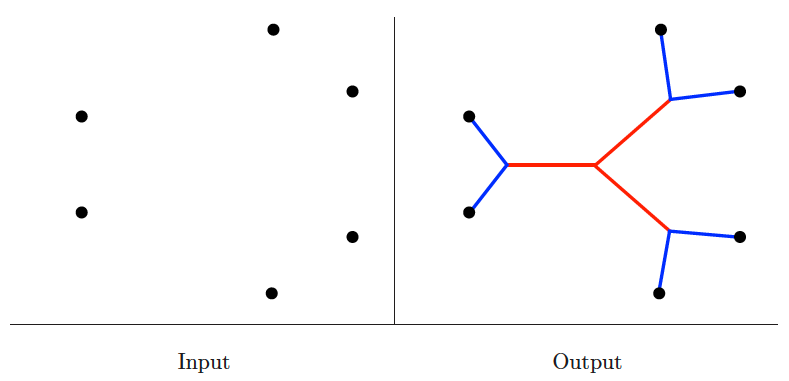
Input description: A graph $G=(V,E)$ and specified subset of vertices $T\subseteq V$. Or set of geometric points $T$.

Problem description:

Feedback edge/vertex set

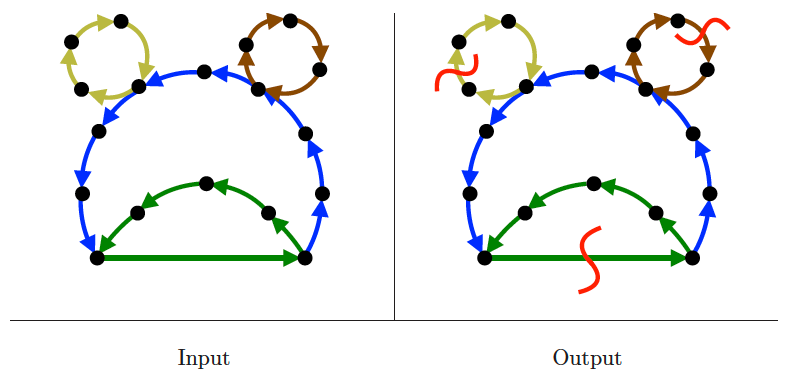
Input description: A (directed) graph $G=(V,E)$.

Problem description: What is the smallest set of edges $E'$ or vertices $V'$ whose deletion leaves an acyclic graph?

Computational geometry

Robust geometric primitives

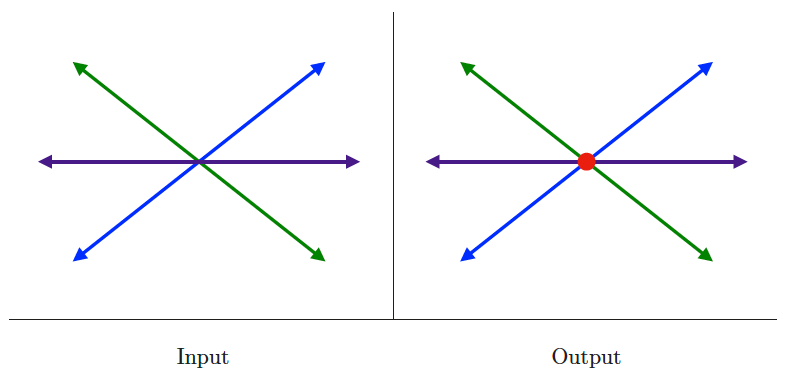
Input description: A point $p$ and line segment $\ell$, or two segments $\ell_1$, $\ell_2$.

Problem description: Does $p$ lie on, over, or under $\ell$? Does $\ell_1$ intersect $\ell_2$?

Convex hull

Input description: A set $S$ of $n$ points in $d$-dimensional space.

Problem description: Find the smallest convex polygon (or polyhedron) containing all the points of $S$.

Triangulation

Input description: A set of points, a polygon, or a polyhedron.

Problem description: Partition the interior of the point set or polyhedron into triangles.

Voronoi diagrams

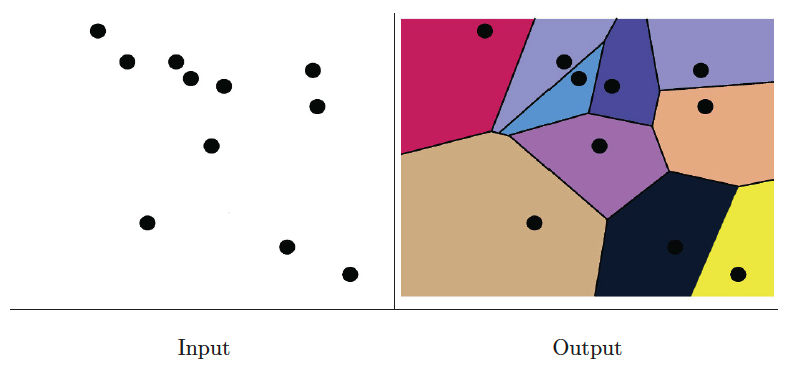
Input description: A set $S$ of points $p_1,\ldots,p_n$.

Problem description: Decompose space into regions such that all points in the region around $p_i$ are closer to $p_i$ than to any other point in $S$.

Nearest-neighbor search

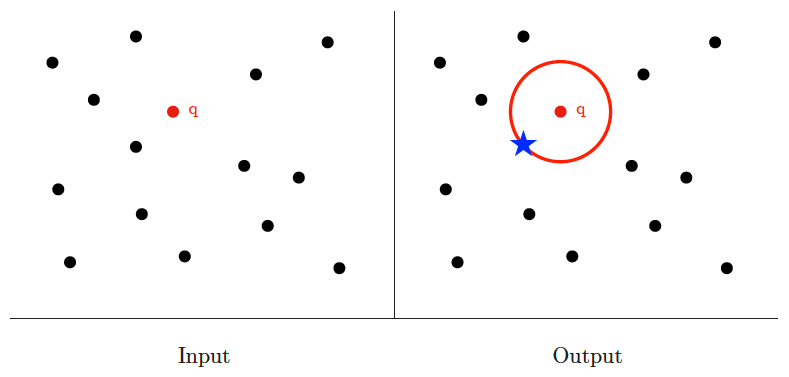
Input description: A set $S$ of $n$ points in $d$ dimensions, and query point $q$.

Problem description: Which point in $S$ is closest to $q$?

Range search

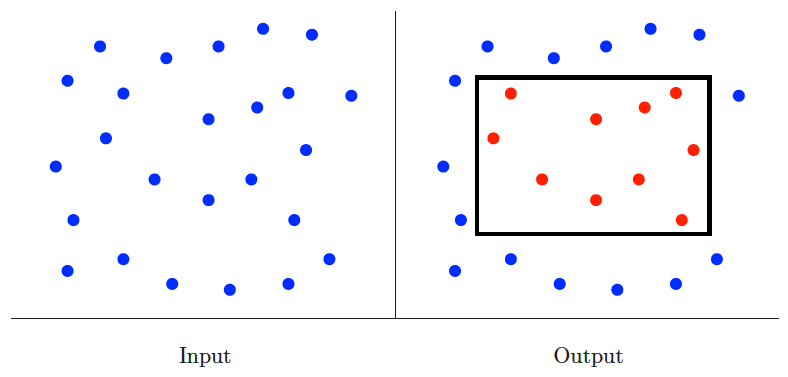
Input description: A set $S$ of $n$ points in $d$ dimensions, and a query region $Q$.

Problem description: Which points in $S$ lie within $Q$?

Point location

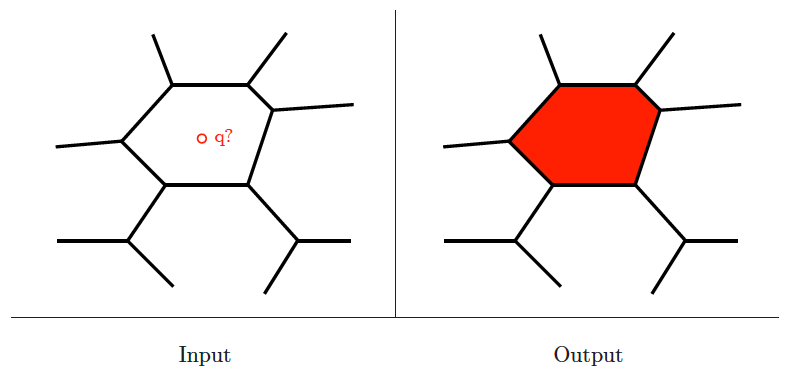
Input description: A decomposition of the plane into polygonal regions, and a query point $q$.

Problem description: Which region contains the query point $q$?

Intersection detection

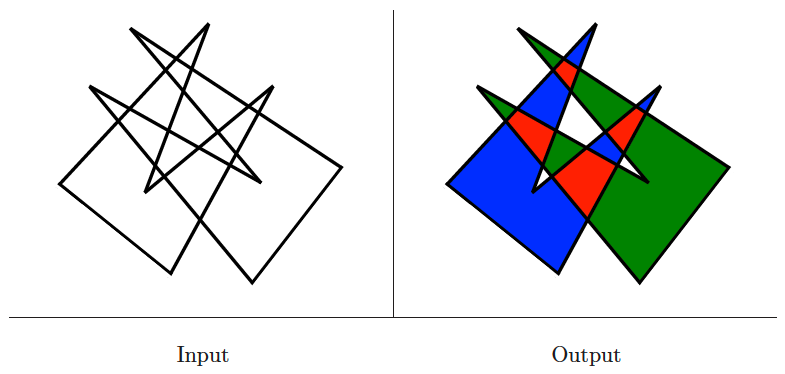
Input description: A set $S$ of lines and line segments $\ell_1,\ldots,\ell_n$, or a pair of polygons or polyhedra $P_1$ and $P_2$.

Problem description: Which pairs of line segments intersect each other? What is the intersection of $P_1$ and $P_2$.

Bin packing

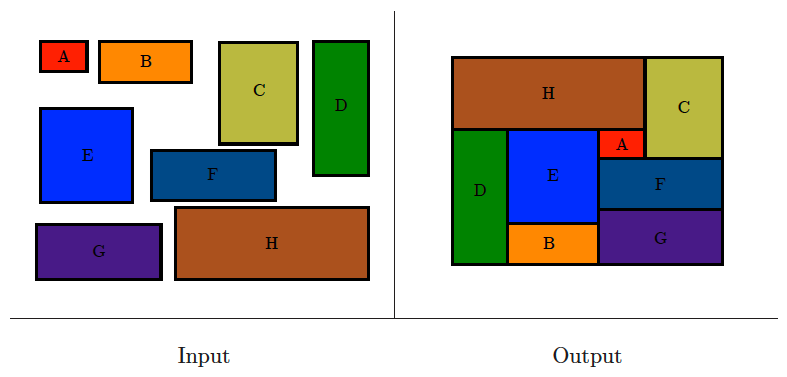
Input description: A set of $n$ items with sizes $d_1,\ldots,d_n$. A set of $m$ bins with capacities $c_1,\ldots,c_m$.

Problem description: Store all the items using the fewest number of bins.

Medial-axis transform

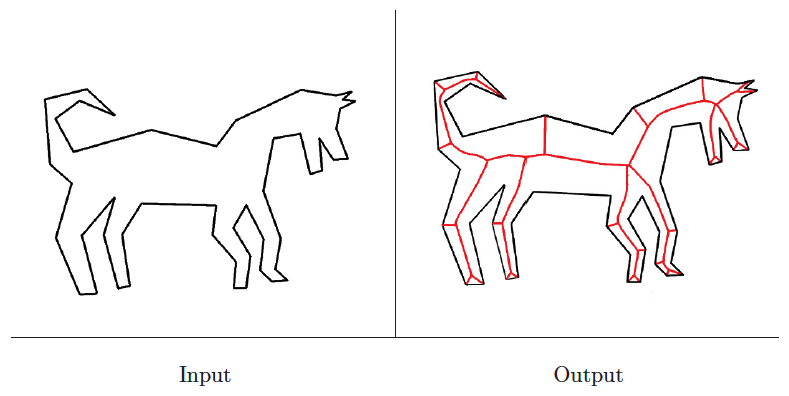
Input description: A polygon or polyhedron $P$.

Problem description: Find the skeleton of $P$, the set of points that have more than one closest point on the boundary of $P$.

Polygon partitioning

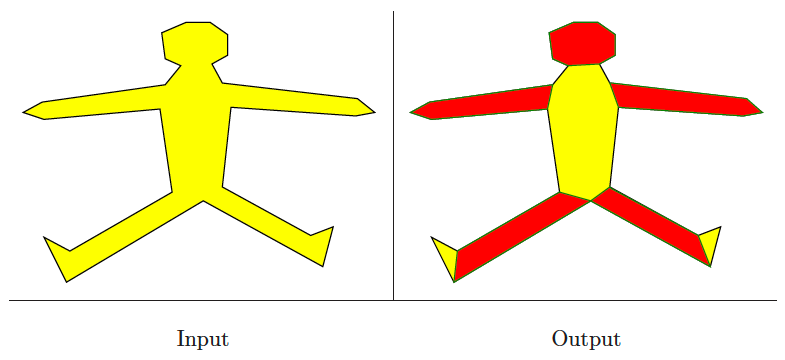
Input description: A polygon or polyhedron $P$.

Problem description: Partition $P$ into a small number of simple (typically convex) pieces.

Simplifying polygons

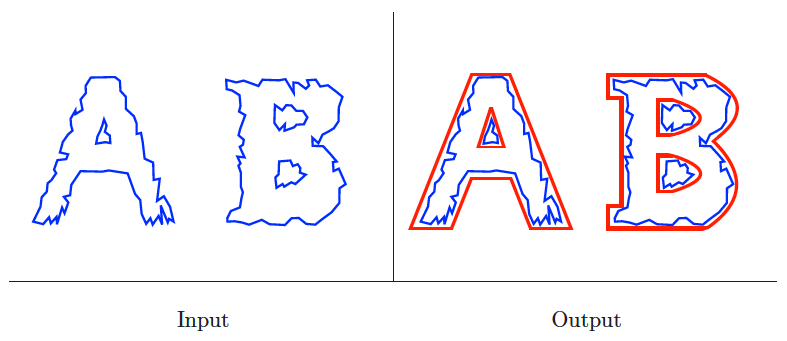
Input description: A polygon or polyhedron $p$, with $n$ vertices.

Problem description: Find a polygon or polyhedron $p'$ containing only $n'$ vertices, such that the shape of $p'$ is as close as possible to $p$.

Shape similarity

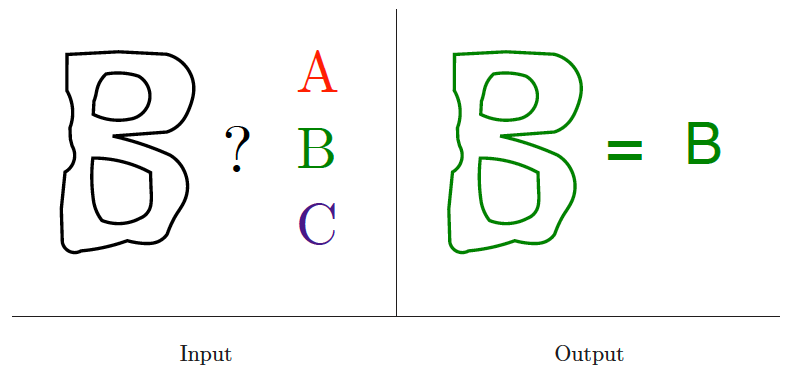
Input description: Two polygonal shapes, $P_1$ and $P_2$.

Problem description: How similar are $P_1$ and $P_2$.

Motion planning

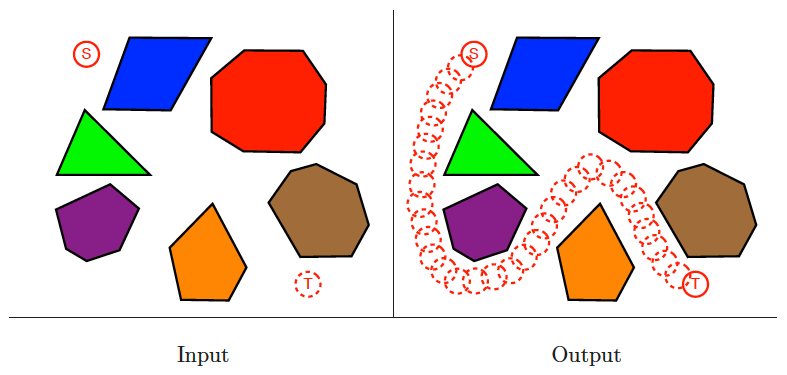
Input description: A polygonal-shaped robot starting at position $s$ in a room containing polygonal obstacles, and a goal position $t$.

Problem description: Find the shortest route taking $s$ to $t$ without intersecting any obstacles.

Maintaining line arrangements

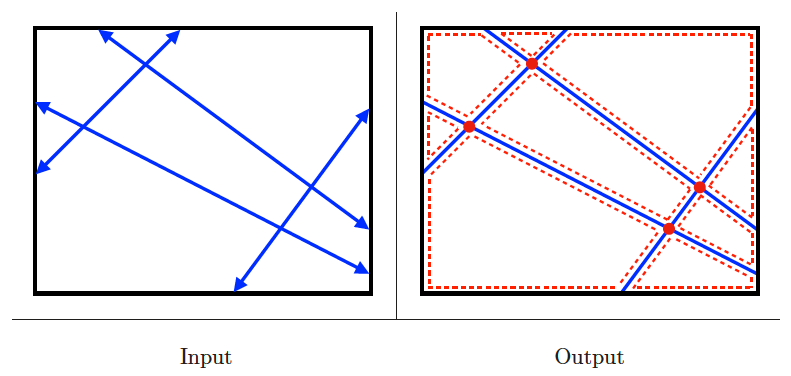
Input description: A set of lines $\ell_1,\ldots,\ell_n$.

Problem description: What is the decomposition of the plane defined by $\ell_1,\ldots,\ell_n$.

Minkowski sum

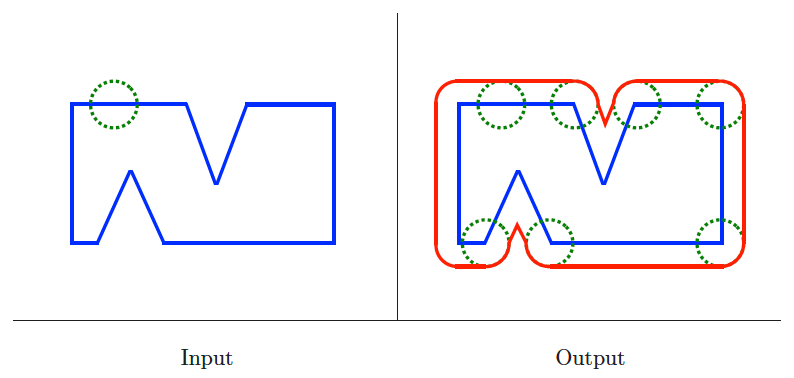
Input description: Point sets or polygons $A$ and $B$, containing $$ and $m$ vertices respectively.

Problem description: What is the convolution of $A$ and $B$, that is, the Minkowski sum $A+B=\{x+y\mid x\in A, y\in B\}$?

Set and string problems

Set cover

Input description: A collection of subsets $S=\{S_1,\ldots,S_m\}$ of the universal set $U=\{1,\ldots,n\}$.

Problem description: What is the smallest subset $T$ of $S$ whose union equals the universal set, that is,

$$\cup_{i=1}^{|T|}T_i=U?$$

Set packing

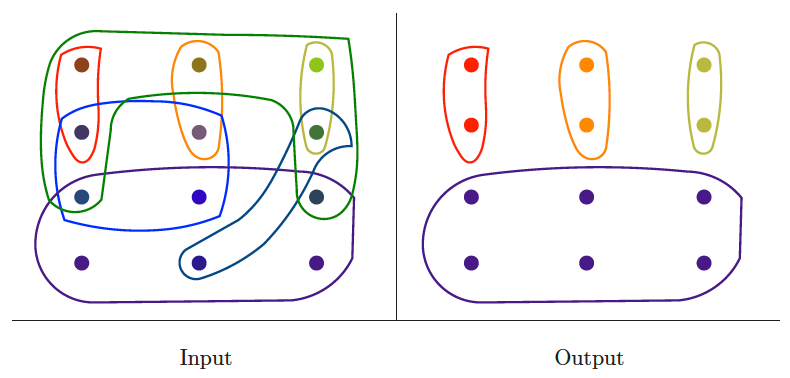
Input description: A collection of subsets $S=\{S_1,\ldots,S_m\}$ of the universal set $U=\{1,\ldots,n\}$.

Problem description: Select a small collection of mutually disjoint subsets from $S$ whose union is the universal set.

String matching

Input description: A text string $t$ of length $n$. A pattern $p$ of length $m$.

Problem description: Find an/all instances of pattern $p$ in the text.

Approximate string matching

Input description: A text string $t$ and a pattern string $p$.

Problem description: What is the minimum-cost way to transform $t$ to $p$ using insertions, deletions, and substitutions?

Text compression

Input description: A text string $S$.

Problem description: Create a shorter text string $S'$ such that $S$ can be correctly reconstructed from $S'$.

Cryptography

Input description: A plaintext message $T$ or encrypted text $E$, and key $k$.

Problem description: Encode $T$ using $k$ giving $E$, or decode $E$ giving $T$.

Fininte state machine minimization

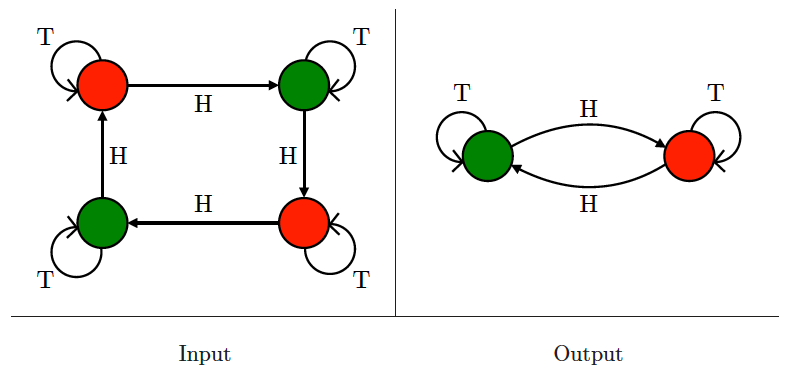
Input description: A deterministic finite automaton $M$.

Problem description: Create the smallest deterministic finite automaton $M'$ such that $M'$ behaves identically to $M$.

Longest common substring/subsequence

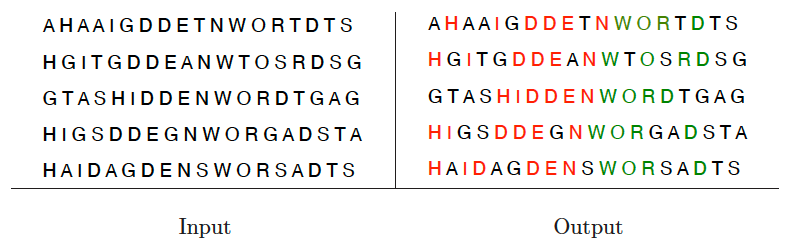
Input description: A set $S$ of strings $S_1,\ldots,S_n$.

Problem description: What is the longest string $S'$ such that all the characters of $S'$ appear as a substring or subsequence of each $S_i$, $1\leq i\leq n$?

Shortest common superstring

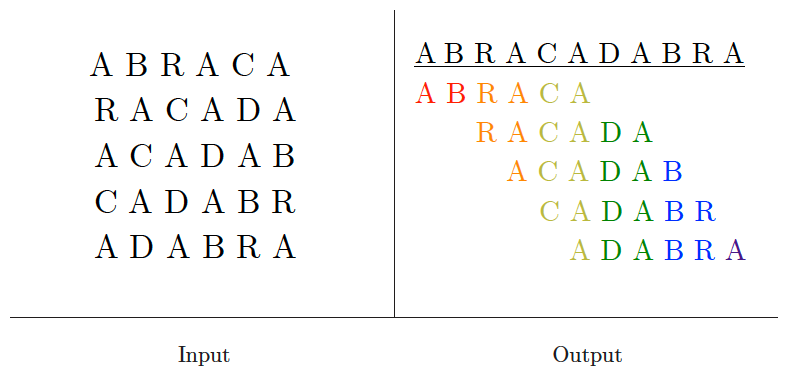
Input description: A set of strings $S=\{S_1,\ldots,S_m\}$.

Problem description: Find the shortest string $S'$ that contains each string $S_i$ as a substring of $S'$.